Umræða og fréttir

Inngangur

Við mat á þýðingu áhættuþátta og tiltekinnar stærðar þarf að byggja á tölfræði. Í greinum sínum vitna höfundar^1,2 í umfjöllun um grein um háhitasvæði og krabbamein³ til hugtaksins Spurious Correlation, sem á íslensku hefur verið þýtt sem dellufylgni. Uppruna hugtaksins má að minnsta kosti rekja til ársins 1926⁴  þegar sýnt var er fram á mikla fylgni á milli dánartíðni (mortality) og markaðshlutdeildar Ensku biskupakirkjunnar í brúðkaupum. Greinin⁴ er kennslubókardæmi þar sem eðli fyrirbærisins er skýrt. Fyrirbærið Spurious Correlation hefur greinilega verið þekkt á þessum tíma því að áður höfðu birst⁵ svipuð rök í greiningu heilsufarsgagna.

Villa sú sem ályktun um tengsl búsetu á háhitasvæðum og krabbameinsáhættu³byggir á er af skyldum toga. Í dellufylgni  liggur villan í því að gögnum er safnað í ákveðnu mynstri sem venjulegar fylgniformúlur taka ekki á. Í greininni um Biskupakirkjuna⁴ er þetta mynstur tímaraðamynstur. Ef gögn eru tímaröðuð er nauðsynlegt að taka tillit til þess mynsturs í ályktunum. Í greininni um háhitasvæðin³ er einnig mynstur. Það mynstur er raðhending (OS: Order Statistics), það er að tíðni krabbameina er raðað. Þegar slík mynstur koma við sögu í fyrirbærum sem stundum er talað um Galton fallacy og/eða Stein paradox. Í grein⁶þar sem meðal annars er athugað nýgengi tiltekins blóðsjúkdóms (toxoplasmosis) í 36 borgum í El Salvador rekja höfundar⁶ kennslubókardæmi með skírskotun til tölfræði um íþróttamenn. Einhver íþróttamaður hlýtur að vinna og sigur hans er samsettur úr heppni og færni. Sama á við um borgirnar 36 í El Salvador. Einhver er óheppnust og hugsanlega eru sumar borgir af einhverjum ástæðum betri/verri. Ýktustu gildin eru sennilega ofmat/vanmat á raunverulegu nýgengi. Í greininni⁶ er fyrirbærið skýrt og stungið upp á endurbættum tölfræðiaðferðum. Hugtakið Galton fallacy er kennt við 19. aldar vísindamanninn Francis Galton sem árið 1877⁷ áttaði sig á því að stórvaxnir foreldrar hafa tilhneigingu til að eignast sér minni afkomendur sem eru þó stærri en meðaleinstaklingurinn. Í nýlegri kennslubók er sagt⁸ að þetta sé oft uppspretta rangra ályktana, Galton fallacy: .. which has been the source of incorrect inferences countless of times.

Þessi grein er þannig byggð upp að fyrst er hugtakið raðhending (OS) skýrt með einföldu dæmi. Síðan er lýst hvernig meta megi áhættuhlutföll (HR: Hazard-Ratio) og hvernig eðlilegt er að matið dreifist. Sýnt er reiknað dæmi sem byggir á einni töflu úr greininni um háhitasvæði.³Byggt er á Taylor-nálgunum á öryggismörkum fyrir áhættuhlutföll. Slíkar nálganir eru alsiða í hagnýtri tölfræði.

Hvað er raðhending (OS: Order Statistics)? Einfalt dæmi

Ef gefnir eru tveir biðtímar T₁ og  T₂ sem báðir eru veldisdreifðar (exponential) slembistærðir (random variable), með meðaltal 1 ár. Þá skilgreinum við T_minsem lægra gildið og T_max  sem stærra gildið. Stærðirnar T_min og T_max eru ekki óháðar. Samkvæmt skilgreiningu þarf að bíða skemur eftir lægra gildinu en hærra gildinu. Með einfaldri líkindafræði er hægt að sjá að væntanlegur biðtími eftir lægra gildinu er 1/2 ár og biðtími eftir hærra gildinu 3/2 ár. Í einföldum tilfellum er eðlilegt að stysti tíminn sé minni en meðaltími (ef hann er til) og að lengsti tími sé stærri en meðaltími. Nánari útfærslur á eiginleikum OS eru skýrðar í kennslubókum eins og til dæmis.⁹

Um talningarbreytur og áhættuhlutföll

Poisson-dreifing er nærtækur kostur til að lýsa fjölda atburða á tilteknu tímabili. Eins og í dæminu um biðtímann er eðlilegt að ef mældar eru margar einsdreifðar óháðar Poisson-breytur með sama meðaltal að þá verði hæsta mæligildið fyrir ofan væntanlegt gildi og það lægsta fyrir neðan. Fyrir Poisson-dreifingu, flestar aðrar dreifingar og hvað þá fyrir hlutföll af slíkum breytum, gildir að ekki eru aðgengilegar nákvæmar formúlur fyrir dreifingu á OS. Því er nauðsynlegt að notast við nálganir eða hermanir til að reikna dreifingu slíkra stærða. Hér er notast við Taylor-nálgun, sem einnig er stundum nefnd delta-aðferð.⁹

Gefnar eru tvær óháðar Poisson-dreifðar hendingar, X₁ og  X₂. Þær lýsa fjölda atburða á tveim jafnfjölmennum svæðum á tilteknu tímabili. Væntanlegur fjöldi atburða af þessari gerð eru λ₁ og  λ₂. Áhættuhlutfallið (HR)=λ₁/λ₂ er áhugaverð stærð. Þess vegna er dreifing stærðarinnar X₁/X₂, áhugaverð en ekki auðreiknanleg með einfaldri líkindafræði. Gróf Taylor-nálgun á dreifni (variance) metins áhættuhlutfalls (gildir ef λ₁ og λ₂ eru stórar tölur) gefur:

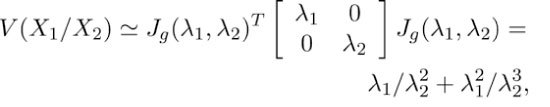(1)

þar sem J_g er Jacobi-afleiða g(x₁,x₂) = x₁/x₂ það er óvissan í reiknuðu HR er háð óvissu í teljara og nefnara.

Einnig mætti hugsa sér að vinna með logaritma HR og þá fæst með Taylor-nálgun að:

V (log(X₁/X₂)) = V (log(X₁) – log(X₂)) ≅ 1/λ₁ + 1/λ₂      

                                                                                                                                            (2)

Nálgun við 95% öryggismörk fyrir HR má því fá með því að beita annaðhvort jöfnu (1) eða (2). Ef λ₁ og  λ₂ eru stórar tölur er útkoman svipuð.

Ef svæðin eru misfjölmenn þarf að samræma kvarðann, til dæmis í nýgengi per 100.000. Þá þarfa að margfalda X_imeð  c_i = 100.000/p_i, þar sem  p_i er stærðin á hóp i. Til að meta breytileika í metnu áhættuhlutfalli þarf því að reikna:

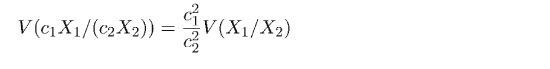
Eðlilegt bilmat á HR (95% öryggismörk) er því annaðhvort

   

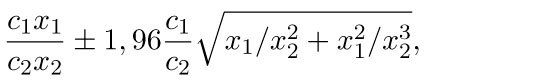
eða

  

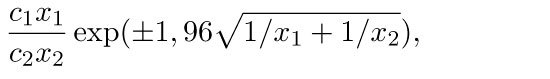
þar sem x₁ og x₂ er mældur fjöldi á svæði 1 og 2.

Dæmi: Ef HR=1 og svæði 2 er 10 sinnum fjölmennara en svæði 1 og mæld eru 10 tilfelli á svæði 1 og 100 tilfelli á svæði 2 eru sennileg öryggismörk samkvæmt jöfnu, (1) (0,35; 1,65) og (0,52; 1,91) samkvæmt jöfnu (2). Jafna (1) hefur þann eiginleika að neðri endi öryggisbilsins getur verið neikvæður og þess vegna er hún minna notuð. Báðar jöfnurnar eru í eðli sínu (bjartsýnar) nálganir og gefa mjög svipuð bil ef til dæmis λ₁ er af stærðargráðunni 100 og  λ₂ af stærðargráðunni 1000.

Í talningargögnum verður að gera ráð fyrir að til staðar sé einhvers konar ofdreifni (OD: overdispersion). Það er að breytileikinn er meiri en samkvæmt Poisson-dreifingunni. Það er því eðlilegt að gera ráð fyrir að öryggismörkin séu að minnsta kosti til dæmis 20-40% breiðari. Hreint Poisson-líkan gefur því bjartsýnasta mögulega mat á nákvæmni. Ef leiðrétta þarf (til dæmis með Cox-aðhvarfsgreiningu) fyrir truflandi breytum, aldri, búsetu, má reikna með að slíkt kosti eitthvað í nákvæmni.

Greinin um háhitasvæðin³ sýnir nokkrar töflur þar sem uppgefið er HR og tilheyrandi öryggisbil. Til dæmis er í töflu III í greininni sagt að mælst hafi 5 tilfelli af briskrabbameini í jarðhitasvæði og að HR sé 2,52 miðað við viðmiðunarsvæði, sem í greininni er kallað warm-reference area. Viðmiðunarsvæðið er um það bil 30 sinnum stærra (667.069/18.181). Hér eru tölurnar 667.069 og 18.181 fjöldi mannára sem samantektin³grundvallast á. Af þessu má ætla að metinn væntanlegur fjöldi tilfella á viðmiðunarsvæði sé 59,5. Ef þessar stærðir eru settar inn í jöfnu (2) fæst nákvæmlega sama bil og í greininni um háhitasvæðið:³

 

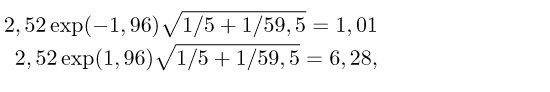
samkvæmt jöfnu (1) fæst bilið (0,22; 4,8). Öryggisbilin í greininni³ virðast reiknuð með jöfnu (2) eða einhverri mjög líkri aðferð.

Ef 20 95% öryggisbil eru reiknuð (gefið að tölfræðilegt líkan sé rétt) má reikna með að um það bil eitt þeirra innihaldi ekki sanna gildið. Í töflunum eru rúmlega 20 bil reiknuð og feitletruð tvö til þrjú sem ekki innihalda HR=1 og gefið í skyn að það sé vísbending um að jarðhiti sé áhættuþáttur fyrir krabbamein.

Hér ber að varast að það sem listað er í töflunum er OS. Óhjákvæmilega er eitt gildið stærst. Ef Z₁, … , Z₂₀eru 20 óháðar staðlaðar normal breytur er væntanlegt hámarksgildi E(max(Z₁, … , Z₂₀)), um það bil 1,86 og tilheyrandi staðalfrávik 0,7.

Ef HR=1 og svæði eitt er það fámennt að að væntanleg tilfelli þar eru 5, og 150 á svæði tvö,  er metið log(HR)/√1/5 + 1/150 um það bil normaldreift með meðaltal 0 og staðalfrávik 1. Því er væntanlegt stærsta log(HR)(meðal 20) um það bil 1,86 √1/5 + 1/150. Með því að nota að væntanlegt gildi log-normaldreifingar er exp(μ + 1/2σ²), mætti áætla að væntanlegt gildi stærsta HR-gildisins meðal 20 krabbameina sem öll hafa HR=1, sé af stærðargráðunni 2,5. Sum krabbameinin í töflu III hafa greinilega væntanlega tíðni sem er minni en 5 á jarðhitasvæðunum.

Ef briskrabbamein í töflu III í greininni³ er skoðað má áætla að væntanlegt gildi á fámenna jarðhitasvæðinu sé tæplega 2 (5/2,52). Ljóst er að ef 20 slík krabbamein eru skoðuð er eðlilegt að stærsta HR-gildi sé enn stærra. Reiknað HR=1 er alls ekki eðlilegur viðmiðunarpunktur í rannsóknum sem þessum (þegar skoða á marga sjúkdóma og væntanlegur fjöldi er lág tala).

Ef λ₁ og λ₂ eru báðar stórar tölur er þessi tegund villu ekki eins sláandi. Þá er (miðað við 20 raðaðar nýgengistölur) 1,86 √1/λ₁ + 1/λ₂ ≅  0 og exp(0)=1 því eðlilegri viðmiðunarpunktur. Marktækni/nákvæmni byggð á öryggismörkum reiknuðum með jöfnum (1) eða (2) verður að sjálfsögðu jafnmisvísandi því gögnin eru OS.

Greinin³ er mjög vel unnin og forvitnileg fyrir þá sem vilja fræðast um Ísland. Ályktunin, það er að gefa í skyn að sum krabbamein séu tíðari á jarðhitasvæðum, hvað þá að um einhvers konar orsakasamband sé að ræða, er fráleit. Greinin sýnir miklu frekar að ástand á jarðhitasvæðum er mjög svipað og á öðrum svæðum. Það er athyglisvert að einungis er skýrt frá þeim krabbameinum þar sem mæld tíðni er stærri en 0 á jarðhitasvæðum. Því er vel hugsanlegt að miklu fleiri en 20 krabbamein hafi verið til skoðunar. Reikna má með að á fjölmennari viðmiðunarsvæðum komi fyrir krabbamein sem mælist með tíðni 0 á jarðhitasvæðum á tímabilinu.

Lokaorð

Þeir útreikningar sem hér hafa verið reifaðir byggja allir á nálgunum (Taylor-nálgunum). Þeir eru þess vegna bjartsýnir og raunveruleikinn sennilega enn öfgakenndari. Annað atriði sem er bjartsýnislegt er að gert er ráð fyrir að talningarferlið fylgi Poisson-dreifingu og að áhættuhlutfallið sé hlutfall tveggja Poisson-dreifðra stærða. Eiginleiki Poisson-dreifðra stærða er að væntanlegt gildi er jafnt dreifninni (varíans). Í mælingum á talningarferlum er algengt að til staðar sé einhvers konar ofdreifni (OD), það er dreifnin er stærri en væntanlegt gildi. Þetta getur orðið til dæmis vegna tískusveiflna eða tækniþróunar í greiningum. Ef gert er ráð fyrir að hlutfall dreifni og væntanlegs gildis sé til dæmis 2, er væntanlegt gildi stærsta HR-gildis rúmir 4 (ef væntanlegur fjöldi fámennara svæðis er 5 og fjölmennara svæðis 150), og staðalfrávik þess væntanlega gildis um það bil 1,9. Miðað við normal nálganir er því ekki hægt að tala um marktækni stærsta HR-gildisins fyrr en HR fer að nálgast 8. Í töflu III í greininni um háhitasvæði³ er einnig vitnað til viðmiðunarsvæðis, cold reference area, og þar er reiknað HR=3,68, það stærsta meðal rúmlega 20 krabbameina.

Dreifing HR milli jarðhitasvæðis og viðmiðunarsvæðis er mjög svipuð því sem vænta mætti, jafnvel þó gert sé ráð fyrir að nýgengi fylgi Poisson-dreifingu. Það er óraunhæft að ætla að nýgengi einstakra krabbameina fylgi Poisson-dreifingu með sama fasta nýgengið í áratugi. Gera verður ráð fyrir sveiflum í tíma, tískusveiflum, tæknisveiflum í greiningum, mannabreytingum í læknastétt og svo framvegis. Því má reikna með að einhvers konar OD sé til staðar. Jafnvel einhver þróun í tíma. Í því ljósi verður að álykta út frá greininni að engin tengsl séu á milli búsetu á jarðhitasvæðum og einstakra krabbameina. Dreifing HR-gilda sem sýnd eru í töflu III í greininni um háhitasvæðið³gefur ekkert annað til kynna.

Heimildir

1. Sigurðsson H, Flóvenz ÓG. Háhitasvæði og krabbamein. Læknablaðið 2015; 101: 276-7.
2. Rafnsson V, Kristbjörnsdóttir A. Háhitasvæði og krabbamein: Svar við umfjöllun Helga Sigurðssonar og Ólafs G. Flóvenz. Læknablaðið 2015; 101: 328-30.
3. Kristbjörnsdóttir A, Rafnsson V. Incidence of cancer among residents of high termperature geothermal areas in Iceland: A census based study 1981 to 2010. Environmental Health 2012; 11: 1-12.
4. Udny Yule G. Why do we sometimes get nonsense-correlations between time-series?  — A study in sampling and the nature of time-series. J Roy Stat Soc 1926; 89: 1-63.
5. Greenwood M, Udny Yule G. An inquiry into the nature of frequency distributions representative of multiple happenings with particular reference to the occurrence of multiple attacks of disease or of repeated accidents. J Roy Stat Soc 1920; 83: 255-79.
6. Efron B, Morris C. Stein's paradox in statistics. Sci Am 1977; 236: 119-27.
7. Galton F. Typical laws of heridity. Nature 1877; 15: 492-5.
8. Leamer EE. Macroeconomic Patterns and Stories. Business and Economics. Springer 2008.
9. Casella G, Berger RL. Statistical Inference second edition. Duxbury, Pacific Grove 2002.