Umræða og fréttir

Það er varla sú rannsókn í heilbrigðisvísindum sem ekki ber saman tvö meðaltöl. Þá kemur traustur vinur til kastanna, gamla góða t-prófið. Eins og öll tilgátupróf byggir t-próf á ákveðnum forsendum en hvað er til ráða þegar þær eru ekki uppfylltar?

T-próf byggir á tveimur forsendum: Að innan hvors hóps séu mælingarnar óháðar og að þær fylgi normaldreifingu. Fyrri forsendan er mikilvæg. Ef mælingarnar eru háðar, t.d. ef innan hóps eru endurteknar mælingar á sömu einstaklingum, er hætta á að villulíkurnar séu meiri en við höldum. Þá þarf að nota flóknari tölfræðiaðferðir sem taka tillit til tengsla mælinganna. Krafan um normaldreifingu er aftur á móti alls ekki eins mikilvæg, sér í lagi ef úrtökin eru stór.

Eitt lögmál tölfræðinnar er það öflugt að á íslensku kallast það höfuðsetning tölfræðinnar. Hún segir að þegar við drögum óháðar mælingar úr einhverri dreifingu, og reiknum meðaltal þeirra, þá nálgast dreifing þessara meðaltala normaldreifingu, sama hver dreifing upprunalegu mælinganna var. Í stuttu máli má segja að meðaltöl verða normaldreifð ef að úrtök eru nógu stór. Um leið og það gerist er t-prófið orðið áreiðanlegt. Því er t-próf ansi þolgott gagnvart frávikum frá normaldreifingu.

Hversu stórt er þá nógu stórt úrtak? Þeim mun frábrugðnari normaldreifingu sem mælingarnar eru, því stærra úrtak þarf, en það kemur á óvart hve lítið úrtak þarf í raun. Á mynd 1 sést stuðlarit af gögnum sem augljóslega eru ekki normaldreifð. Þar við hliðina sjáum við stuðlarit af meðaltölum 30 mælinga sem eru dregnar endurtekið úr sömu gögnum og sjá! Hér er 30 manna úrtak nógu stórt til að meðaltölin verði normaldreifð!

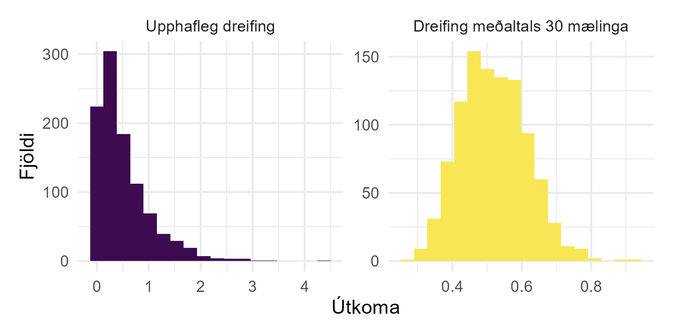
Til vinstri, stuðlarit af mælingum sem fylgja mjög hægri skekktri dreifingu. Til hægri, stuðlarit af meðaltölum 30 mælinga sem eru dregnar endurtekið úr dreifingunni til vinstri. 

Í heilbrigðisvísindum er algengt að mælingar séu skekktar til hægri, til dæmis fjöldi hvítra blóðkorna í blóðsýni, kreatín-gildi eða stærð krabbameinsæxla. Slíkar mælingar fylgja oft svokallaðri logranormaldreifingu, það er, þær verða normaldreifðar ef við tökum náttúrlega logrann af þeim. Þá er þægileg lausn að taka fyrst logra af mælingunum og framkvæma svo t-próf í kjölfarið.

En hvað þá með Mann-Whitney-prófið? Því er oft fleygt fram sem alhliða valkosti til að bera saman miðgildi tveggja hópa en færri vita að prófið byggir líka á ákveðnum forsendum: Að hóparnir hafi svipaða lögun og dreifni. Ef þær forsendur bresta getur prófið verið varasamt og við ranglega haldið að miðgildi séu ólík þegar það er í raun dreifnin sem er frábrugðin. Mann-Whitney er því engin töfralausn og ætti ekki að vera sjálfgefið val.

Þegar allt um þrýtur er eitt próf óupptalið: Umraðanaprófið. Þar notum við upphaflegu gögnin til að búa til hundruð þúsunda gerviúrtaka með því að umraða mælingunum tilviljanakennt í hópana tvo í hvert skipti. Þannig metum við hversu líklegt það er að meðaltölin verði jafn ólík og þau raunverulega eru, ef enginn munur er í raun, og framkvæmum tilgátupróf á þeim grunni. Umraðanapróf gerir enga kröfu um líkindadreifingu mælinga, en er flóknara í framkvæmd og hefur minna afl en t-próf, þegar það á við.

Til vinstri, stuðlarit af mælingum sem fylgja mjög hægri skekktri dreifingu. Til hægri, stuðlarit af meðaltölum 30 mælinga sem eru dregnar endurtekið úr dreifingunni til vinstri. 

T-prófið hefur staðist tímans tönn og er vinsælt af góðri ástæðu. Það er einfalt, þrautseigt og aflmikið. Nú þegar líður að jólum er við hæfi að hugsa hlýtt til gamalla vina. Gleymum því ekki t-prófinu. Það er traustur félagi sem reynist vel á ólíklegustu stundum.